Czy wszystkie życzenia kobiet mogą zostać spełnione?

Pamiętam jak przy okazji grafów dwudzielnych (tzn. takich, gdzie zbiór wierzchołków można rozbić na dwa podzbiory) omawialiśmy twierdzenie Halla (o małżeństwach, tj. o kojarzeniu się małżeństw, także wersję haremową). Był to jeden z tematów, który wspominam z sentymentem. Dlaczego? Zapraszam na wpis, w którym matematyka odpowie na pytanie: czy wszystkie życzenia kobiet mogą zostać spełnine? 😉

Tematy grafowe chyba przypadły wam do gustu. Jeśli pierwszy raz spotykasz się z takimi zadaniami wpadnij na wpis odpowiadający na pytanie co to jest graf? co to jest reprezentacja maszynowa grafu?.

Twierdzenie Halla o małżeństwach

Hall w swoim twierdzeniu skojarzenia w grafie porównał do kojarzenia się par. Przy czym to każda kobieta ze zbioru wybiera sobie jednego lub kilku spośród dostępnych mężczyzn (mężczyźni w tym wypadku nie mieli nic do gadania 😉 ).

Według twierdzenia Halla może dojść do małżeństwa, jeżeli dowolna podgrupa kobiet oznaczona jako r chciałaby poślubić co najmniej r-mężczyzn.

Prościej mówiąć – potrzebna jest przynajmniej taka sama liczba mężczyzn, co liczba kobiet w dowolnej podgrupie. Jest to warunek konieczny i wystarczający, żeby skojarzyć pary.

gdzie:
k – oznacza liczbę kobiet
m – oznacza liczbę mężczyzn
k większe lub równe 1
m większe lub równe 1
m większe lub równe k

Jak to rozumieć? Odejdźmy od małżeństw i grafów. Załóżmy, że mamy 4 trenerów pokemonów. Każdy z nich szuka jednego lub więcej pokemonów, ale akurat dzisiaj każdy z nich ma ze sobą tylko 1 pusty pokeball (może złapać tylko 1 pokemona, mam nadzieję, że nic nie pokręciłam 😉 ).

Tak wygląda graf dwudzielny: trenerzy – pokemony, które chcą złapać.

Dodajmy, że trenerzy nie będą walczyć między sobą o pokemony, pokemonów jest dosyć, by każdy dostał jednego. Jak widać, można utworzyć skojarzenia między trenerami, a pokemonami, tak by każdy trener miał swojego pokemona.

Zgodnie z twierdzeniem: jeśli weźmiemy dowolną podgrupę trenerów to przypadnie na nich conajmniej tyle samo pokemonów. Biorąc trzech dowolnych trenerów, musimy mieć 3 lub więcej potencjalnych pokemonów do złapania.

Tak się rozpisałam, a pominęłam najważniejsze przesłanie z zajęć!

Matematyka to jednak czasem ma bardzo praktyczne podejście do życia ^^.

Szybki podsumowanie i zadania:
Następujący graf A będzie grafem dwudzielnym i ma skojarzenie:

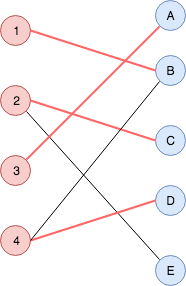
ale graf B jest grafem dwudzielnym, ale skojarzenia nie ma:

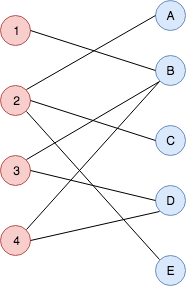
ponieważ dla 3 wierzchołków: {1,3,4} znane są tylko 2 wierzchołki: {B, D}.

Zadania

Czas na zadanie praktyczne!
Napisz program, który

• wczytuje graf z pliku tekstowego
• sprawdza, czy graf jest grafem dwudzielnym,
• jeżeli graf jest grafem dwudzielnym, sprawdź, czy istnieje skojarzenie,
• zwróć wynik sprawdzenia
• graf ma skojarzenie, zwróć skojarzone pary

Testowanie programu:
Stwórz kilka przypadków testowych (instancji):
– kilka grafów dwudzielnych i innych
– utwórz instancje małe (10 wierzchołków), średnie (14-20 wirzechołków) i duże (ok. 25 wierzchołków)