Kilka słów o grafach sprzężonych, wrzucam trochę opracowanej teorii, w bardziej przystępnej formie.
Wpis dla tych co marudzili, że na blogu zadania są za proste, dlatego dzisiaj trochę większa gimnastyka umysłu!
Post ze szczególną dedykacją dla bioinformatyki – zawsze pozostanie w moim sercu 😉.
Przed lekturą tego posta polecam zapoznać się z pojęciem teorii grafów i podstawami reprezentacji maszynowej grafów.
Czym jest graf sprzężony?
Na to pytanie nie da się prosto odpowiedzieć bez wprowadzenia kilku podstawowych pojęć.
Graf nieskierowany – krawędzie między wierzchołkami są bezkierunkowe.
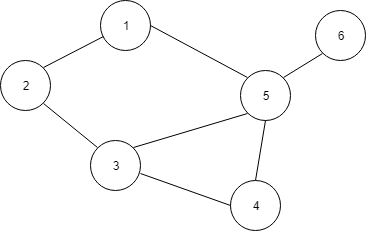
Graf skierowany – jego łuki między wierzchołkami mają zwroty (znamy kierunek).
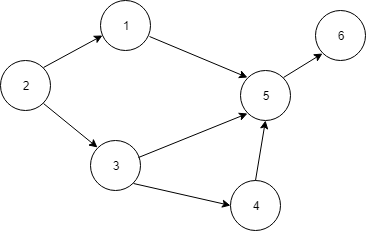
Typy grafów
- 1 – graf – to taki który nie ma łuków wielokrotnych
- multigraf – graf mogący mieć łuki wielokrotne (między 1 -> 5 łuk wielkorotny)

1-graf
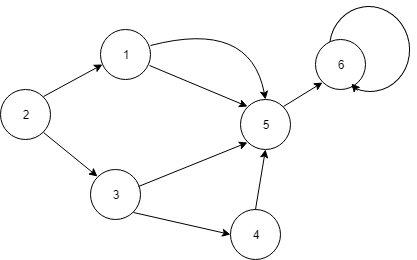
Multigraf
Graf sprzężony – definicja
Graf sprzężony G (adjoint) G = (V, A) grafu skierowanego H = (U, V) – jest 1-grafem, którego wierzchołki reprezentują łuki z H, i który posiada łuk od x do y, jeśli w H wierzchołek końcowy łuku x jest wierzchołkiem początkowym łuku y.
Ufff…tyle z definicji podręcznikowej.
Czym właściwie jest to nieszczęsne sprzężenie czy też graf sprzężony?
Spróbuję napisać to prościej. Graf sprzężony to graf, którego wierzchołki są odwzorowaniem łuków grafu H (to nie jest oficjalna definicja, ale jej przyjazna wersja a teraz obrazek poniżej).
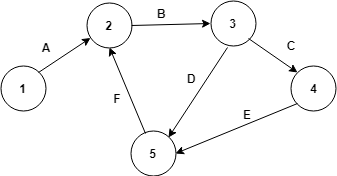
Graf oryginalny (U, V)
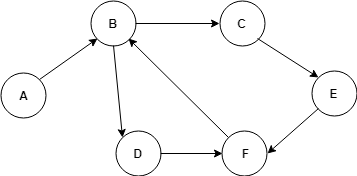
Graf sprzężony (V, A)
1) W grafie oryginalnym łuk A wchodzi do wierzchołka, z którego wychodzi łuk B, dlatego w grafie sprzężonym istnieje łuk łączący wierzchołek A → B
2) Łuk B wchodzi do wierzchołka, z którego wychodzą dwa łuki: C i D. stąd w grafie sprzężonym mamy wierzchołek B połączony skierowaną krawędzią z wierzchołkiem C i z wierzchołkiem D.
…i tak dalej
Jak łatwo zauważyć:
Graf sprzężony ZAWSZE jest 1-grafem, podczas gdy graf oryginalny może być multigrafem.
Kolejny warunek, aby graf mógł być uznany za graf sprzężony:
Graf G = (V, A) jest grafem sprzężonym wtedy i tylko wtedy, gdy następująca własność jest spełniona dla każdej pary x,y ∈ V:
gdzie N+(x) jest zbiorem następników x, a N+(y) jest zbiorem następników y.
A teraz po ludzku: aby graf G był naszym grafem sprzężonym musi mieć powyższą właściwość, czyli:
- porównujemy następniki dla dowolnej pary wierzchołków
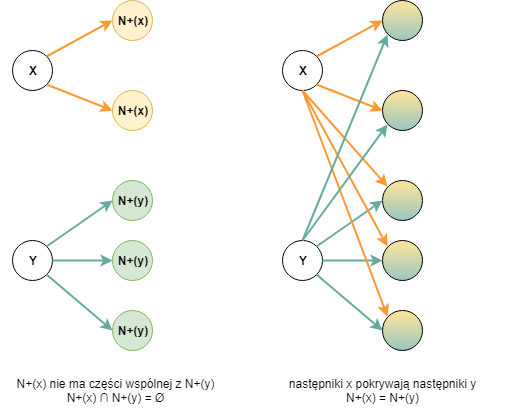
- zbiór tych następników musi być pusty (zbiory rozłączne). A jeśli jest nie pusty ( warunek : N+(x) ∩ N+(y) ≠ Ø ) to implikuje to zależność, że wszystkie następniki x muszą pokrywać się z wszystkimi następnikami y
Poniższa ilustracja powinna trochę rozjaśnić:
Graf liniowy to graf sprzężony grafu oryginalnego, który jest 1-grafem.
Jeśli graf sprzężony nie zwiera żadnej z poniżej wymienionych struktur to jest on grafem liniowym. Na tej podstawie wiemy, że jego graf oryginalny był 1-grafem, a nie multigrafem.

Szczęśliwie nie trzeba tego tworzyć od podstaw. W książce „Wybrane algorytmy i modele grafowe w bioinformatyce” M. Kasprzak (egzemplarz dostępny w bibliotece Politechniki Poznańskiej) rozdział 3 „Sekwencjonowanie” str. 42, znajdziemy następującą zależność:
1-graf G jest skierowanym grafem liniowym, wtedy i tylko wtedy, gdy dla wszystkich jego par wierzchołków x i y spełniony jest warunek:
gdzie N–(x) oznacza zbiór bezpośrednich poprzedników x.

Aby dowiedzieć się, czy graf oryginalny był 1-grafem wystarczy sprawdzić, czy powyższy warunek jest spełniony dla naszego grafu sprzężonego. To już jest znacznie przyjemniejsze do zakodzenia niż sprawdzanie struktu.
PS: Jakby ktoś miał do sprzedania „Wybrane algorytmy i modele grafowe w bioinformatyce” M. Kasprzak, chętnie odkupię! Mam do tej pozycji ogromny sentyment 🙂
Grafy – zadania
Zadanie, które miałam na studiach, a które można wykonać po lekturze tego posta dla własnej satysfakcji 😉
Zaimplementuj dokładny algorytm [o złożoności wielomianowej], który
- wczytuje graf z pliku tekstowego
- sprawdza, czy graf jest grafem sprzężonym,
- jeżeli graf jest grafem sprzężonym, sprawdź, czy jest jednocześnie grafem liniowym,
- zwróć wynik sprawdzenia
- graf sprzężony przekształć w graf oryginalny (H),
zapisz graf wynikowy do nowego pliku tekstowego
Testowanie programu:
Stwórz kilka przypadków testowych (instancji):
– kilka grafów sprzężonych (część też jako grafy liniowe), kilka, które grafami sprzężonymi być nie mogą
– utwórz instancje małe (5 wierzchołków), średnie (7-10 wirzechołków) i duże (12-15 wierzchołków)
Za mało zadań?
Sprawdź ponad 1000 zadań w Pythonie (lub dowolnym języku programowania)


Świetny blog, będę go śledził. Czy jesteś na bieżąco z osiągnięciami bioinformatyki? Byłabyś w stanie podać trzy najbardziej fascynujące osiągnięcia ostatniego roku?
Dość ciekawe pytanie – bioinformatyka zazwyczaj łączy się z innymi dziedzinami badania / analizy mogą być na użytek biologii molekularnej, genomiki czy projektowania leków. Wszystkie aktualizacje wydawane przez Nanopore są osiągnięciami bioinformatycznymi ( poprawa jakości sekwencjonowania danych genomowych). Rzucałabym okiem na postępy w algorytmach mapowania etc, ale to nie są takie ekscytujące odkrycia jak nowy lek na raka czy łazik marsjański. Odkryć bioinformatyki często nie widać, ale są wykorzystywane w innych dziedzinach np. odkrycie zupełnie nowej formy przenoszenia informacji – circRNA (krótki, kuliste RNA) będzie odkryciem bioinformatycznym a znalezienie korelacji konkretnych cząsteczek circRNA z jednostkami chorobowymi bardziej wpasujemy w medycynę, mimo że stoi za tym ogromna analiza bioinformatyczna i cała praca mokrego labu – biotechnologiczna. Na pewno badania nad CRISPR w tak zaawansowanym stanie są zasługą bioinformatyki. Jeśli powiesz mi w jakim konretnie obszarze np. genomika roślin, medycyna, czy biorobotyka – mogę poszukać konkretych narzędzi, metod, odkryć z ostatnich 10 lat.
Skomplikowane to, muszę więcej czasu na to poświęcić… ;p
Zastanawia mnie jak ostatecznie powinien wyglądać taki kod, ponieważ mam problem z jego napisaniem. Czy mogę liczyć na pomoc i wyjaśnienie?